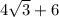Answer:
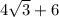
Explanation:
We know that the base is 6 and the altitude is
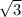
We need to know the sides of the triangle
The triangle is already divided into two by the altitude, the new base will be 3 because 6 divided by 2 is 3, and the side of the smaller triangle will be
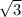
So we use the pythagoream thereom:
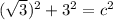
Now since we are squaring a square root, it goes back to 3, and we know
 equals 9:
equals 9:
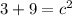
Now we solve:
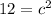
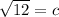
Now we know the side of the triangle ABC
Since it is an isosceles, both sides are
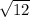
Now we add all sides to get our perimeter: P=
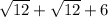
We know that
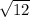 +
+
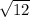 =
=
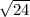 =
=
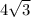 .......when we factor
.......when we factor
Which is: