Answer:
The speed of the plane is:
200 mph
Explanation:
Mattie Evans drove 150 miles in the same amount of time that it took a turbopropeller plane to travel 600 miles.
Let the time taken be t.
Hence, the speed of car is: 150/t
( Since, the speed is the ratio of distance traveled to the time taken )
and the speed of plane is: 600/t
Also, it is given that:
The speed of the plane was 150 mph faster than the speed of the car.
i.e.
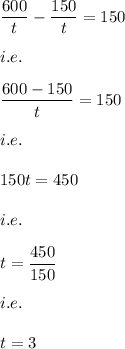
Hence, the speed of the plane is:
