Question

Select all the correct locations on the table.

The table below contains points on an exponential function, f. Select the two points in the table which create an interval with an average rate of change of -60.

Answer 1

1 and 5

Explanation:

Since, the rate of change of function f(x) between a to b is
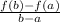`(f(b)-f(a))/(b-a)` or
`(f(a)-f(b))/(a-b)`

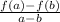
Given,

f(1) = 27, f(2) = 21, f(3) = 3, f(4) = -51 and f(5) = -213,

Thus, the rate of change between 1 and 2 =
`(f(2)-f(1))/(2-1)=(21-27)/(2)=(-6)/(2)=-3`

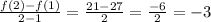
Similarly,

The rate of change, between 1 and 3 = -12,

between 1 and 4 = -26,

between 1 and 5 = -60,

between 2 and 3 = -18,

between 2 and 4 = -36,

between 2 and 5 = 78,

between 3 and 4 = -54,

between 3 and 5 = -108,

between 4 and 5 = -162

Hence, the point in the table that create an interval with the rate of change -60 are,

1 and 5.

Answer 2

Average rate of change: r=[f(b)-f(a)]/(b-a)

r=-60→[f(b)-f(a)]/(b-a)=-60

b=5; f(b)=-213; a=1; f(a)=27
(-213-27)/(5-1)=(-240)/4=-60

Answer: The two points in the table which create an interval with an average rate of change of -60 are:
x f(x)
1 27
5 -213