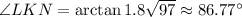Question

PLS HELP ME!!!!!!!! 99 POINTS

Given: KLMN is a trapezoid,
KL = MN
LN = 89 ,
LH- altitude
LM = 3, KN = 13.
Find: m∠LKN

Answer 1

`\angle LKN=\arctan1.8√(97)\approx 86.77^(\circ)`

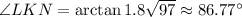
Explanation:

Draw the second altitude MB (see attached diagram).

Quadrilateral HLMB is a rectangle, then LM = HB = 3 units.

Trapezoid KLMN is isosceles trapezoid (because KL=MN), thus

`KH = BN = (KN-HB)/(2)=(13-3)/(2)=5\ units\\ \\HN=HB+BN=3+5=8\ units`

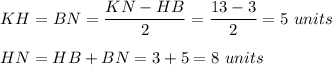
Triangle LHN is right triangle, then by Pythagorean theorem,

`LN^2=LH^2+HN^2\\ \\89^2=LH^2+8^2\\ \\LH^2=89^2-8^2\\ \\LH^2=(89-8)(89+8)\\ \\LH^2=81\cdot 97\\ \\LH=9√(97)\ units`

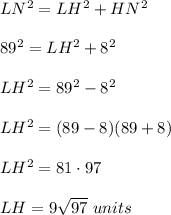
Consider right triangle KLH. In this triangle,

`\tan\angle LKH=\{\tan\angle LKH\}=\frac{\text{opposite leg}}{\text{adjacent leg}}=(LH)/(KH)=(9√(97))/(5)=1.8√(97)\ units`

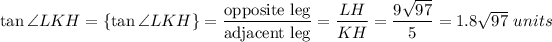
So,

`\angle LKN=\arctan1.8√(97)\approx 86.77^(\circ)`