Answer:
$41,770.55
Explanation:
Compound Interest Formula
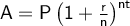
where:
- A = Final amount.
- P = Principal amount.
- r = Interest rate (in decimal form).
- n = Number of times interest is applied per year.
- t = Time (in years).
Given values:
- A = $50,000
- r = 2.25% = 0.0225
- n = 12 (monthly)
- t = 8 years
Substitute the given values into the formula and solve for P:
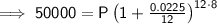
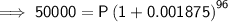
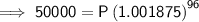
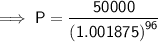
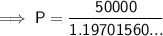
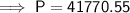
Therefore, Matilda should deposit $41,770.55.