Question

a regular heptagon has a radius of approximately 27.87cm and the lengthof each side is 24.18cm. what is the approximate area of the heptagon rounded to the nearest whole number? recall that a polygon with 7 sides. A. 1,173 squared cm. B. 2,125 squared cm. C. 2,359 squared cm. D. 4,250 squared cm.

Answer 1

The Answer is B: 2,125 cm²


n = 7
a = 24.18 cm
r = 25.1051 cm
R = 27.8646 cm
A = 2124.65 cm²
P = 169.26 cm
x = 128.571 °
y = 51.4286 °


Agenda:
r = inradius (apothem)
R = circumradius
a = side length
n = number of sides
x = interior angle
y = exterior angle
A = area
P = perimeter
π = pi = 3.14159...
√ = square root

Formula: A = (1/4)na2 cot(π/n) = nr2 tan(π/n)

Answer 2

The correct option is: B. 2,125 squared cm.

Explanation:

Formula for the Area of a regular polygon is......

`A= (1)/(2)r^2 n\ sin((360)/(n))`

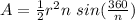
where,
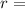`r=` radius,
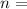`n=` number of sides.

Here the polygon is a regular heptagon with radius of 27.87 cm.

That means,
`n=7,\ \ r= 27.87\ cm`

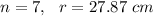
Plugging these values into the above formula........

`A=(1)/(2)(27.87)^2(7)\ sin((360)/(7))\\ \\ A=(1)/(2)(776.7369)(7)(0.7818)\\ \\ A=2125.4707... \approx 2125\ (rounded\ to\ nearest\ whole\ number)`

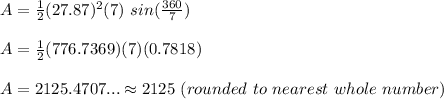
So, the approximate area of the heptagon will be 2125 squared cm.