Question

If the circle (x - 5)2 + (y - 3)2 = 6 is translated 4 units to the left and 1 unit up, what is the center of the circle? A) (-9, -2) B) (-4, -7) C) (1, 4) D) (6, -1)

Answer 1

Answer: The correct option is (C) (1, 4).

Step-by-step explanation: The given equation of the circle is

`(x-5)^2+(y-3)^2=6.`

The standard equation of a circle with center (g, h) and radius 'r' units is given by

`(x-g)^2+(y-h)^2=r^2.`

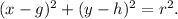
Comparing equation (i) with the standard equation, we get that the center of the circle (i) is (5, 3).

After a translation of 4 units to the left, the co-ordinates of the center becomes

(5-4, 3) = (1, 4).

After a translation of 1 unit up, the co-ordinates of the center will be

(1, 3+1) = (1, 4).

Therefore, the final co-ordinates of the center are (1, 4).

Thus, (C) is the correct option.

Answer 2

The center of the given circle is (5, 3). Adding (-4, 1) to its coordinates will put it at (1, 4).

C) (1, 4)