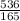Question

How to convert 3.248 repeating decimal with 48 repeating into a simplified fraction

Answer 1

`(536)/(165)`

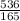
Explanation:

Step 1: let's call
`x` the repeating decimal.

So,
`x=32.2484848484848...`

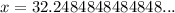
Step 2: identify the number of digits that repeats.

We see that two digits repeat 4 and 8.

Step 3: multiply 100 at each side of the equation, two digits, two zeros, that's why is 100.

`100x=324.84848484848...`

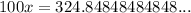
Step 4: we subtract the repeating decimal the last expression:

`100x-x=(324.8484848...)-(3.2484848...)\\99x=321.6`

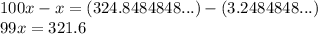
Step 5: solve for
`x`.

`x=(321.6)/(99)`

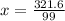
In this case, we have to multiply each part of the fraction by 10 to get rid of the decimal number.

`x=(321.6(10))/(99(10))=(3216)/(990)=(536)/(165)`

Therefore, the repeating decimal is equal to
`(536)/(165)`

Answer 2

`x=(536)/(165)`

Explanation:

Let X be the value of 3.2484848.... infinite times

Multiply by 100

`x=3.24848....\\100x = 324.8484.....`

Subtract to get

`100x-x = 324.8484...-3.248484....\\99x = 321.60\\x=(321.6)/(99) \\x=(1072)/(330) \\x=(536)/(165)`

Thus the number 3.248 repeating decimal with 48 repeating in fraction form is

`(536)/(165)`