Question

A proton moves perpendicular to a uniform magnetic field b at a speed of 1.80 107 m/s and experiences an acceleration of 1.90 1013 m/s2 in the positive x direction when its velocity is in the positive z direction. determine the magnitude and direction of the field.

Answer 1

1) The magnetic force exerted on the proton, since it is moving perpendicular to the magnetic field, is

`F=qvB`
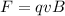
where q is the proton charge, v its velocity and B the intensity of the magnetic field.
Since the proton is moving by circular motion, this force is equal to the centripetal force:

`F=qvB=ma_c`
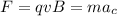
where m is the proton mass and ac is the centripetal acceleration.

Substituting the data of the problem and re-arranging the formula, we find:

`B= (ma_c)/(qv)= ((1.67 \cdot 10^(-27) kg)(1.90 \cdot 10^(13) m/s^2))/((1.6 \cdot 10^(-19) C)(1.80 \cdot 10^7 m/s))= 0.011 T`
so, the magnitude of the magnetic field is 0.011 T.

2) Direction:
the direction of the magnetic field can be found by using the right-hand rule.
Let's take:
- the index finger as the direction of the velocity (positive z-direction)
- the middle finger as the direction of the magnetic field
- the thumb as the direction of the force (which has same direction as the acceleration) (positive x-direction)
we can see that by using the right hand, the middle finger points toward negative y-direction, so the magnetic field is in the negative y-direction.