Question

The prime factorization of a number is 3^2x5^3x7. Which statement is true about the factors of the number? ? Twenty-one is a factor of the number because both 3 and 7 are prime factors. Twenty-one is not a factor of the number because 21 is not prime. Ninety is a factor of the number because 3^2=9 and 90 is divisible by 9. Ninety is not a factor of the number because 90 is not divisible by 7.

Answer 1

Twenty-one is a factor of the number because both 3 and 7 are prime factors.

Explanation:

Given number is,

`3^2* 5^3* 7`

`=3* 3* 5* 5* 5* 7`

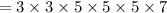
Where, 3, 5 and 7 are prime numbers ( only divisible by 1 and itself ),

⇒ Both 3 and 7 are prime factors of the given number,

⇒ 21 is a factor of the given number.

Thus, first option is correct.

⇒ Second option is incorrect.

Now, 5 is factor of the given number but 2 is not,

⇒ 10 is not a factor of the given number,

⇒ 90 is not a factor of the given number,

⇒ Third option is incorrect.

Suppose 90 is divisible by 7,

⇒ 90 = 7a

Where a is any whole number,

⇒
`7=(90)/(a)`

`3^2* 5^3* 7=3^2* 5^3* (90)/(a)`

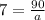
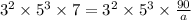
Since, 90 could be a factor of this number, if a = 3 or 5 or their multiple,

For the other values of a, 90 can not be the factor,

Hence, there is no effect of divisibility of 90 by 7 on having 90 as a factor of the given number,

⇒ Fourth option is incorrect.

Answer 2

The 1st statement is true.

21 is a factor because both 3 and 7 are factors.