The information tells us that (3x+1)²=9(x-2)², so this means that we must now solve this equation to find x.
First, we expand the parentheses on both sides using FOIL (Firsts, Outers, Inners, Lasts) :
(3x+1)(3x+1)=9(x-2)(x-2)
9x²+3x+3x+1=9(x²-2x-2x+4
Simplify:
9x²+6x+1=9(x²-4x+4)
Now expand the RHS (right-hand side) expression - multiply all the terms inside the parentheses by 9:
9x²+6x+1=9x²-36x+36
Now solve as you normally would to isolate x. Start off by subtracting 9x² on both sides:
6x+1=-36x+36
Add 36x on both sides:
42x+1=36
Minus 1 on both sides:
42x=35
Divide both sides by 42:

which simplifies to
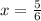
I double checked this by substituting x back into the question and it worked, you can try doing this too for verification.