Question

In the function y=5x^2-2, what effect does the number 5 have on the graph, as compared to the graph of y=x^2?

A.it shrinks the graph vertically by a factor of 5
B. it stretches the graph horizontally by a factor of 5
C.it stretches the graph vertically by a factor of 5
D.it shrinks the graph horizontally by a factor of 5

Answer 1

C.it stretches the graph vertically by a factor of 5

Answer 2

General Idea:

The Rules for Transformations of Functions are given below:

If f(x) is the original function, a > 0 and c > 0; Then

`f(x)+k \; \; shift \; f(x) \; UPWARD \; k \; units\\\\f(x)-k \; \; shift \; f(x) \; DOWNWARD \; k \; units\\\\f(x+h) \; \; shift \; f(x) \; LEFT \; h \; units\\\\f(x-h) \; \; shift \; f(x) \; RIGHT \; h \; units\\\\-f(x) \; \; REFLECT \; f(x) \; in \; the \; x-axis\\\\f(-x) \; REFLECT \; f(x) \; in \; the \; y-axis\\\\a \cdot f(x), \; a>1 \; STRETCH \; f(x) \; vertically \; by \; a \; factor \; of \; a\\\\a \cdot f(x), \; 0<a<1 \; SHRINK \; f(x) \; vertically \; by \; a \; factor \; of \; a\\\\`

`f(ax), \; a>1 \; SHRINK \; f(x) \; horizontally \; by \; a \; factor \; of \;(1)/(a) .\\\\f(ax), \; 0<a<1 \; STRETCH \; f(x) \; horizontally \; by \; a \; factor \; of \;(1)/(a)`

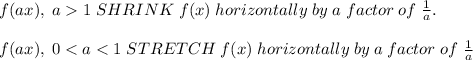
Applying the concept:

In the function y=5x^2-2, the effect that the number 5 have on the graph, as compared to the graph of y=x^2 is given below:

C.it stretches the graph vertically by a factor of 5