Question

In the figure below, the segment is parallel to one side of the triangle. Find the value of x.

Answer 1

18 2/3

Explanation:

It was correct on my assignment

Answer 2

Answer: x= .
`18(2)/(3)`.

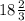Step-by-step explanation: We are given a segment parallel to the base.

Therefore, sides of big triangle and small triangles would be in proportion.

`(One \ Side \ of\ big \ triangle )/(One \ Side \ of\ small \ triangle) =(Other \ Side \ of\ big \ triangle )/(Other \ Side \ of\ small \ triangle)`

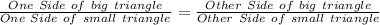
Setting values for the shown triangle, we get

`(x+(x+7))/(x) =(16+22)/(22)`

`(2x+7)/(x) =(38)/(16)`

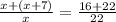
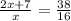
On cross multiplication, we get

16(2x+7) = 38(x)

32x + 112 = 38x.

Subtracting 112 from both sides, we get

32x + 112-112 = 38x -112

32x = 38x-112

Subtracting 38x from both sides, we get

32x-38x = 38x-38x-112

-6x = -112

Dividing both sides by -6, we get

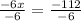
`(-6x)/(-6) =(-112)/(-6)`

x= .
`18(2)/(3)`.

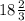Therefore, x= .
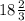`18(2)/(3)`.