Question

Help please! Identify an equation in point slope form for the line perpendicular to Y =-2x + 8 that passes through (-3, 9)

Answer 1

easy bruh

y-y1=m(x-x1) is the point slope formula

your (x1,y1) is the given point. (-3,9).

you know that the slope is m=-2 because the slope of the line is right there. so you need to have the multiplicative inverse for it to be the perpindicular slope. that is 1/2.

now just plug in your numbers into the point slope for formula.

y-9=1/2(x-(-3))
y-9=1/2x+3/2

Answer 2

Point-slope form of the required line is
`(y-9)=(1)/(2)(x+3)`.

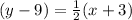Explanation:

We have the equation of the line as 'y=-2x+8'.

On comparing with the general form of the line given by 'y=mx+b', where m is the slope, gives that the slope of this equation is -2.

As we know, 'If two lines are perpendicular, then the product of their slopes is -1'.

Thus, we have,
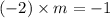`(-2)* m=-1`, where m is the slope of the required line.

Then,
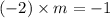`(-2)* m=-1` i.e. -2m = -1 i.e.
`m=(1)/(2)`.

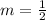We know, the point-slope form is given by,
`(y-y_(1))=m(x-x_(1))`

Since, the lines passes through (-3,9).

We have, the point-slope form of the required line is
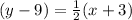`(y-9)=(1)/(2)(x+3)`.