Question

Need help with Part A

Answer 1

`z=(8+pi)/(p-4i)`
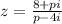
given Re(z)=2/5

Part (a) to find the possible values of p.

1. we rationalize z by multiplying the denominator by it's conjugate

`z=(8+pi)/(p-4i)`

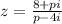
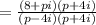
`=((8+pi)(p+4i))/((p-4i)(p+4i))` ]multiple top & bottom by conjugate of denominator]

`=((8+pi)(p+4i))/((p-4i)(p+4i))`

`=(4p+(p^2+32)i)/(p^2+16)`

`=(4p)/(p^2+16)+((p^2+32))/(p^2+16)i`

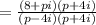
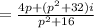
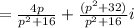
2. The real part is therefore
`=(4p)/(p^2+16)`
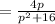
and we have been given that Re(z)=2/5.
We now form the equation

`(4p)/(p^2+16)=2/5`
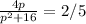
which transforms to the quadratic equation

`2(p^2+16)-20p=0`
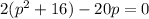
and simplifies to

`p^2-10p+16=0`
and factors to

`(p-8)(p-2)=0`
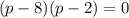
and using the zero product property, we deduce that

p=8 or p=2

Check:
substitute p=8 in z gives
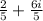
`(2)/(5)+(6i)/(5)` ....good
substitute p=2 in z gives
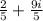
`(2)/(5)+(9i)/(5)` ....good

If you need help with the other parts, please let me know.