Answer:
0.0436m
Step-by-step explanation:
The potential (V) of a point charge (Q) at a distance (r) is given by;
V = k x Q / r ------------------(i)
Where;
k = constant = 9 x 10⁹ Nm²/C²
[A] Now,
(i) let's get the distance (r₁) from the charge with the 2000V equipotential as follows;
2000 = k Q / r₁
Make r₁ subject of the formula as follows;
r₁ = k Q / 2000
Therefore the distance r₁ of the 2000V equipotential surface from the charge is kQ / 2000
(ii) let's get the distance (r₂) from the charge with the 3000V equipotential as follows;
3000 = k Q / r₂
Make r₂ subject of the formula as follows;
r₂ = k Q / 3000
Therefore the distance r₂ of the 3000V equipotential surface from the charge is kQ / 3000
[B] To get how much farther (r) from the charge the 2000V equipotential surface is than the 3000V, we find the difference between r₁ and r₂ as follows;
r = r₁ - r₂ ------------------(ii)
Where;
r₁ = k Q / 2000
r₂ = k Q / 3000
Substitute these values into equation (ii) as follows;
r =
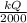 -
-
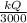
Solve for r;
r = 0.0005kQ - 0.0003kQ
r = kQ (0.0005 - 0.000333)
r = kQ (0.000167)
Now substitute the values of k and Q = 29n C (29 x 10⁻⁹C) into the equation above as follows;
r = 9 x 10⁹ x 29 x 10⁻⁹ x 0.000167
r = 0.0436m
Therefore, the 2000V equipotential surface is 0.0436m from the 3000V surface.