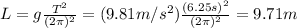Question

Find the length of a pendulum that oscillates with a frequency of 0.16 hz. the acceleration due to gravity is 9.81 m/s 2 . answer in units of m.

Answer 1

The period of the pendulum is the reciprocal of the frequency:

`T= (1)/(f)= (1)/(0.16 Hz)=6.25 s`

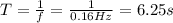
The period of the pendulum is given by

`T=2 \pi (L)/(g)`
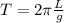
where L is the length of the pendulum, and g the acceleration of gravity. By re-arranging the formula and using the value of T we found before, we can calculate the length of the pendulum L:

`L=g (T^2)/((2 \pi)^2)=(9.81 m/s^2) ((6.25 s)^2)/((2 \pi)^2)=9.71 m`