Question

Alex's friends have collected 180 gold coins to give to charity. Alex decides he wants to donate some gold coins also, so he adds some gold coins to the 180 that his friends have already collected. Alex decides he must donate an integer number of coins which will make up between 10% and 20%, inclusive, of the total number of gold coins donated. What is the difference between the maximum number of gold coins Alex can donate and the minimum number of gold coins he can donate?

Answer 1

25

Explanation:

If Alex donates x gold coins, then there are 180+x gold coins, and the fraction of gold coins contributed by Alex is
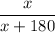`$(x)/(x+180)$`. We then know that

`\[(1)/(10) \le (x)/(x+180) \le (1)/(5).\]`To figure out the values of x satisfying this inequality, we need to look at the solutions to the inequality
`$(1)/(10) \le (x)/(x+180)$` that are also solutions to the inequality
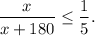`$(x)/(x+180) \le (1)/(5).$` For the first inequality, since 10(x+180) is positive, multiplying both sides by 10(x+180) gives

`$(x)/(x+180) \le (1)/(5).$`

`\Rightarrow \qquad x+180 & \le 10x \\`

`\Rightarrow \qquad 180 & \le 9x \\`

`\Rightarrow \qquad 20 & \le x.`

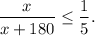
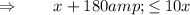
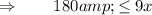
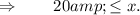
Therefore, the minimum number of coins Alex can donate is 20. Similarly, to solve the inequality
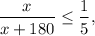`$(x)/(x+180) \le (1)/(5),$` we can multiply both sides by 5(x+180) (since this is positive) to get

`(x)/(x+180) &\le (1)/(5) \\\Rightarrow \qquad 5x & \le x+180 \\\Rightarrow \qquad 4x & \le 180 \\\Rightarrow \qquad x & \le 45.`

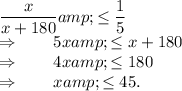
Therefore, the maximum number of coins that Alex can donate is 45. The answer is therefore 45-20 =
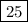`\boxed{25}`.

Answer 2

9/10=180/x
x=200

8/10=180/x
(180*10)/8
(180*5)/4
x= 225

225-200=25
Answer: 25
I THINK