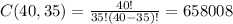Answer:
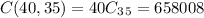
Explanation:
We can use Combinatorics in order to solve this problem. Combinatorics is the part of Mathematics that studies the various ways of grouping with the elements of a set, forming them and calculating their number. There are different ways of making these groupings. Depending on whether the elements are repeated or not, we can use a permutation or a combination.
A permutation of a set of elements is an arrangement of said elements taking into account the order. A combination of a set of elements is a selection of those elements regardless of order. In this case, the order doesn't matter, hence, this is a combination. The number of k-permutations of n elements is given by:
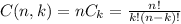
Where:
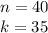
Therefore, the different groups that can be formed are: