Question

Another 20 Points...

The equation for the circle is:
x2+y2+16x−24y+159=0 .

What is the center of the circle?
Enter your answer in the boxes.

( , )

Answer 1

x^2 + 16x + 64 + y^2 - 24y + 144 = -159 + 64 + 144
(x +8)^2 + (y - 12)^2 = 49
Center: (-8,12)

Answer 2

Explanation:

alright lets get started.

We have given the equation of the circle as

`x^2+y^2+16x-24y+159=0`

adding and subtracting 64 from above equation

`x^2+y^2+16x-24y+159+64-64=0`

`x^2+16x+64+y^2-24y+95=0`

`(x+8)^2+y^2-24y+95=0`

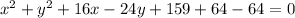
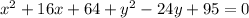
adding and subtracting 144 from above equation

`(x+8)^2+y^2-24y+95+144-144=0`

`(x+8)^2+(y-12)^2-49=0`

`(x+8)^2+(y-12)^2=49`

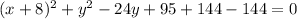
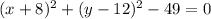
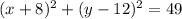
Hence, this is the standard form of circle equation,

So, the center of the circle will be (-8,12). answer

Hope it will help.