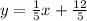Question

What is the equation of the line that is parallel to the given line and passes through the point (-2,2)

Answer 1

First we need to find the equation of the line that is given:

We can use the formula,
`m= ( y_(1) - y_(2) )/( x_(1) - x_(2) )`


`(-3-(-4))/(0-(-5))` =
`(1)/(5)`

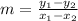
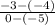
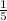
So the equation for this line is
`y= (1)/(5) x - 3`

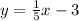
This means that the equation for the line we are trying to find has a slope of
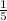
`(1)/(5)` as well

Lets put in the points in the equation and try to find the y-intercept:


`2= (1)/(5) (-2) +b`

`(12)/(5) =b`

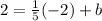
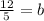
So the final equation for the line we are trying to find is:


`y= (1)/(5)x+ (12)/(5)`