Answer:
422.39 square units.
Explanation:
We have been given that a 3×10, rectangle sits inside a circle with radius of 12. We are asked to find the area of shaded region.
The area of shaded region will be equal to the area of circle minus area of the rectangle.
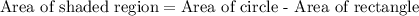
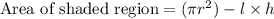 , where,
, where,
r = Radius of circle,
l = Length of rectangle,
b = Height of rectangle.
Upon substituting our given values in above equation we will get,
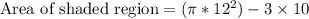
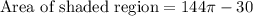
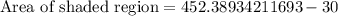
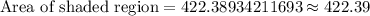
Therefore, the area of shaded region will be approximately 422.39 square units.