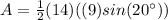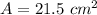Answer:
The area of triangle PQR is
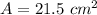
Explanation:
we know that
The area of a triangle is equal to
see the attached figure to better understand the problem
we have
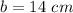
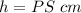
Find the length side of segment PS
In the right triangle PSR
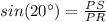
Solve for PS
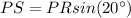
we have
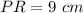
substitute
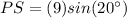
Find the area of the triangle PQR