Answer:
Explanation:
From the given figure, it can be seen that the coordinates of the given points are:
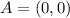 ,
,
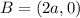 ,
,
 ,
,
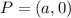 ,
,
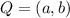 ,
,
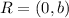 .
.
Now, The coordinates of P, Q and R are:
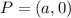 ,
,
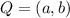 ,
,
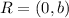 .
.
Now, slope of PQ is given as:
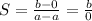
which is undefined.
Slope of RQ is given as:
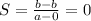
which are the required slope of PQ and RQ respectively.