Question

Prove: Every point on the perpendicular bisector of a segment is equidistant from the ends of the segment.

AP = BP

(fill in the blanks of the equation in the second picture with the correct number/letter/sign based off the first picture.)

Answer 1

AP=√(a² + b² )
BP=√(a² + b² )

Answer 2

Answer with explanation:

Here ,let line, x=0 intersect ,segment AB at point M.

So, PM ⊥ AB.

And, AM =BM →→→∵ y axis or segment PM , is Perpendicular bisector of segment AB.

In Δ AMP and ΔB MP

∠AMP = ∠ B MP=90°[→→ Each being 90°]

AM = BM →Line PM , is perpendicular Bisector.

Side MP , is Common.

Δ AMP ≅ ΔB MP→→→[S AS]

So, AP= BP →→[C P C T]

2. We will use distance formula to find AP and BP.

Distance between two points
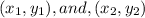`(x_(1),y_(1)), and ,(x_(2),y_(2))` is given by
`=\sqrt{(x_(2)-x_(1))^2+(y_(2)-y_(1))^2`

`AP=√((-a-0)^2+(0-b)^2)\\\\ AP=√(a^2+b^2)\\\\ BP=√((a-0)^2+(0-b)^2)\\\\ BP=√(a^2+b^2)`

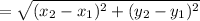
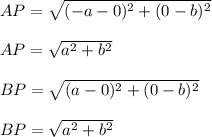
Hence, AP = BP

Where ,Point P, can be located anywhere on y axis.