Question

−8x+44≥60 AND−4x+50<58

Answer 1

The set of inequalities have no solution.

Explanation:

We are given two inequalities:

`-8x+44\geq 60 \\-4x+50<58`

Solving the two inequalities, we have:

`-8x+44\geq 60\\-8x+44-44\geq 60-44\\-8x \geq 16\\\displaystyle(-8x)/(-8) \leq (16)/(-8)\\\\x \leq -2\\\text{In interval notation, we can write,}\\x \in (-\infty, -2]`

`-4x+50<58\\-4x +50-50 < 58-50\\-4x < 8\\\displaystyle(-4x)/(-4) > (8)/(-4)\\\\x > -2\\\text{In interval notion we can write,}\\x \in (-2, \infty)`

For the solution of both the inequalities, we have

`x \in (-\infty,-2] \cap (-2,\infty) = \phi`

Thus,the set of inequalities have no common solution, hence, no solution.

Answer 2

No Solution

Explanation:

`-8x+44\geq 60 and  -4x+50<58`

WE solve each inequality separately then we combine the answers

`-8x+44\geq 60`

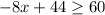
Subtract 44 from both sides

`-8x\geq 16`

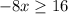
Divide by
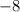`-8` on both sides , when we divide by negatie number then we flip the inequality sign

`x \leq -2`

now solve the other inequality

`-4x+50<58`

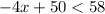
Subtract 50 on both sides

`-4x<8`

Divide by
`-4`

`x > -2`

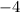
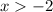
Consider both inequlities

`x \leq -2` and
`x > -2`

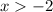
There is no intersection between both inequalities

So no solution