Question

The data show the average monthly temperatures for two cities over a 6-month period. City 1: {20, 24, 40, 63, 76, 89} City 2: {41, 50, 58, 62, 72, 83} What does the mean absolute deviation (MAD) of the data sets tell you about the temperatures over the 6-month period? Select from the drop-down menus to correctly answer the question. The MAD for City 2 is _______ the MAD for City 1, which means the average monthly temperatures of City 2 vary _______ the average monthly temperatures for City 1.

Answer 1

The MAD for City 2 is less than the MAD for City 1, which means the average monthly temperatures of City 2 vary less than the average monthly temperatures for City 1.

Explanation:

The given data sets are

City 1 : {20, 24, 40, 63, 76, 89}

City 2 : {41, 50, 58, 62, 72, 83}

Formula for mean:

`Mean=(\sum x)/(n)`

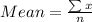
Mean of city 1 is

`Mean=(20+24+40+63+76+89)/(6)=52`

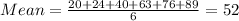
Mean of city 2 is

`Mean=(41+50+58+62+72+83)/(6)=61`

Formula for mean absolute deviation:

`MAD=(\sum |x-\mu|)/(n)`

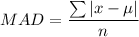
where, μ is the mean of data.

MAD for City 1:

`MAD=(|20-52|+|24-52|+|40-52|+|63-52|+|76-52|+|89-52|)/(6)`

`MAD=24`

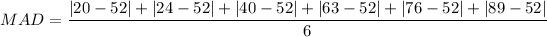
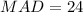
MAD for City 2

`MAD=(\left|41-61\right|+\left|50-61\right|+\left|58-61\right|+\left|62-61\right|+\left|72-61\right|+\left|83-61\right|)/(6)`

`MAD=\approx 11.33`

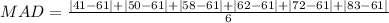
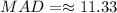
From the above calculation we get 24 > 11.33 or MAD of city 1 > MAD of city 2.

The MAD for City 2 is less than the MAD for City 1, which means the average monthly temperatures of City 2 vary less than the average monthly temperatures for City 1.

Answer 2

The MAD of city 2 is less than the MAD for city 1, which means the average monthly temperature of city 2 vary less than the average monthly temperatures for City 1.

Explanation:

For comparing the mean absolute deviations of both data sets we have to calculate the mean absolute deviation for both data sets first,

So for city 1:

`Mean = x1 = (20+24+40+63+76+89)/(6)`

`x1 = (312)/(6)`

`x1 = 52`

Now to calculate the mean deviations mean will be subtracted from each data value. (Note: The minus sign is ignored as the deviation is the distance of value from the mean and it cannot be negative. For this purpose absolute is used)

`20-52 = -32=32\\24-52=-28=28\\40-52=-12=12\\63-52=11\\76-52=24\\89-52=37`

The deviations will be added then.
`Mean Absolute Deviation = (32+28+12+11+24+37)/(6) \\=(144)/(6)\\=24`

So the mean absolute deviation for city 1 is 24 ..

For city 2:

`Mean = x2 = (41+50+58+62+72+83)/(6)`

`x2 = (366)/(6)`

`x2 = 61`

Now to calculate the mean deviations mean will be subtracted from each data value. (Note: The minus sign is ignored)

`41-61=-20=20\\50-61=-11=11\\58-61=-3=3\\62-61=1\\72-61=11\\83-61=22`

The deviations will be added then.
`Mean Absolute Deviation = (20+11+3+1+11+22)/(6) \\=(68)/(6)\\=11.33`

So the MAD for city 2 is 11.33 ..

So,

The MAD of city 2 is less than the MAD for city 1, which means the average monthly temperature of city 2 vary less than the average monthly temperatures for City 1.