Question

BEFORE YOU CLICK THIS I have asked for help with this like 5 times and people have been answering it with the random word just to get points pls move on if you're not going to help me

Arrange the parabolas represented by the equations in order of the positions of their directrixes on the coordinate plane, starting with the lowest and ending with the highest.

Answer 1

The order of equation is

`y=(1)/(8)x^2-(1)/(2)x-(1)/(2)`

`y=-(1)/(12)x^2-(7)/(6)x-(109)/(12)`

`y=-(1)/(32)x^2-(1)/(16)x-(289)/(32)`

`y=(1)/(20)x^2+(2)/(5)x+(29)/(5)`

`y=-(1)/(16)x^2+(3)/(4)x-(21)/(4)`

`y=(1)/(8)x^2+(3)/(4)x+(41)/(8)`

`y=-(1)/(52)x^2-(4)/(13)x-(146)/(13)`

`y=(1)/(28)x^2-(5)/(14)x+(333)/(28)`

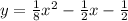
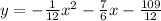
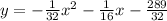
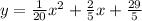
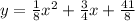
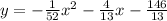
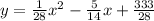
Explanation:

If a parabola is defined as

`y=ax^2+bx+c`

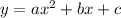
then the directrix of the parabola is

`y=-(b^2)/(4a)-(1)/(4a)+c`

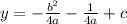
1.

The equation of the parabola is

`y=(1)/(8)x^2+(3)/(4)x+(41)/(8)`

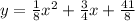
The directrix of the parabola is

`y=-(((3)/(4))^2)/(4((1)/(8)))-(1)/(4((1)/(8)))+((41)/(8))`

`y=2`

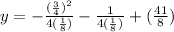
Similarly find the directrix of each parabola.

2.

The equation of the parabola is

`y=(1)/(20)x^2+(2)/(5)x+(29)/(5)`

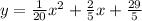
The directrix of the parabola is
`y=0`

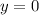
3.

The equation of the parabola is

`y=-(1)/(52)x^2-(4)/(13)x-(146)/(13)`

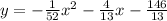
The directrix of the parabola is
`y=3`

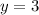
4.

The equation of the parabola is

`y=-(1)/(16)x^2+(3)/(4)x-(21)/(4)`

The directrix of the parabola is
`y=1`

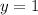
5.

The equation of the parabola is

`y=(1)/(8)x^2-(1)/(2)x-(1)/(2)`

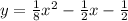
The directrix of the parabola is y=-3.

6.

The equation of the parabola is

`y=-(1)/(32)x^2-(1)/(16)x-(289)/(32)`

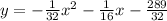
The directrix of the parabola is y=-1.

7.

The equation of the parabola is

`y=-(1)/(12)x^2-(7)/(6)x-(109)/(12)`

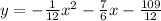
The directrix of the parabola is y=-2.

8.

The equation of the parabola is

`y=(1)/(28)x^2-(5)/(14)x+(333)/(28)`

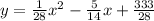
The directrix of the parabola is y=4.

Answer 2

see the attached picture for the correct order: