Question

What transformation has changed the parent function f(x) = log5 x to its new appearance shown in the graph below? logarithmic graph passing through point negative 1, negative 2.

f(x + 2) + 2
f(x + 2) − 2
f(x + 2) + 5
f(x − 2) − 5

Answer 1

F(x+2)-2 is the correct answer. I got it right on my test. Just make sure the point passing through is -1,-2 or you will miss this question. Hope I help you all.

Answer 2

B. f(x + 2) − 2

Explanation:

We are given the function
`f(x)=\log_(5)x`.

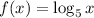Now, f(x) is transformed to obtain a function passing through the point (-1,-2).

So, we get that,

Translating the logarithm function by 2 units to the left and then 2 units downwards.

We get the function
`f(x)=\log_(5)(x+2)-2`.

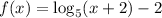So, on substituting the value x= -1, we get,

`f(-1)=\log_(5)(-1+2)-2`

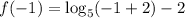
i.e.
`f(-1)=\log_(5)(1)-2`

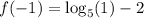
i.e.
`f(-1)=-2`

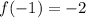
Thus, the function
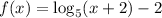`f(x)=\log_(5)(x+2)-2` passes through the given point as shown below.

So, the required transformation is f(x + 2) − 2.