Question

The number of animals in a population is 775, and it increases by of 51% each year.

a. Model the situation with an exponential function.

b. Find how many animals there will be in 10 years.

c. How many years will it take for the population to become 1150.

Show all work!

Answer 1

Answer(a):

Exponential growth formula is given by

`A=P(1+r)^t`

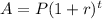
Where preset population = P= 775

Rate of increase = r = 51% = 0.51

t= number of years

A= Future value.

Plug these values into above formula:

`A=775(1+0.51)^t`

`A=775(1.51)^t`

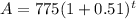
Hence required exponential function is
`A=775(1.51)^t`

Answer(b):

plug t=10 years

`A=775(1.51)^t=775(1.51)^(10)=775(61.6267795034)=47760.7541151`

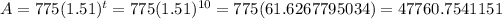
which is approx 47761.

Answer(c):

Plug A=1150

`1150=775(1.51)^t`

`(1150)/(775)=(1.51)^t`

`\ln((1150)/(775))=t*\ln(1.51)`

`0.394654192004=t*0.412109650827`

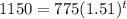
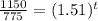
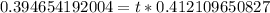
0.957643654334=t

Which is approx 1 year.