Question

Describe the nature of the equation 4x²-12x+9=0​

Answer 1

Given equation is
`4x^(2)-12x+9=0`

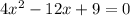
To find nature of roots , we need to find Discriminant,D =
`b^(2)-4ax`

now , from comparing equation with the general equation of quadratic form ,
`ax^(2)+bx+c=0`

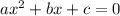
We get , a = 4 , b = -12 , c = 9

Now finding discriminant , D = b^2-4ac substituting the values we get,

D = (-12)^2 - 4(4)(9)

=> D = 144-144 = 0

If D = 0 then the roots are rational and equal roots occur.

To find them we can use -b/2a , -b/2a

If D>0 then roots are real and unequal

If D<0 there are no real roots , complex roots (imaginary roots exist)

If D= 0 roots and real and equal.

Answer 2

Quadratic equation because it equals 0