Question

Long division
3x+1/6x^6+5x^5+2x^4-9x^3+7x^2-10x+2

Answer 1

`(6 x^(6)+5x^(5)+2x^(4)-9x^(3)+7x^(2)-10x+2) / (3x+1)`

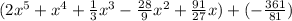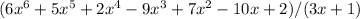
We divide first number from first parenthesis with first number from second parenthesis. Then the resulting number we multiply by all numbers in second parenthesis and substract from first parenthesis.


`6 x^(6)/3x = 2 x^(5) \\ \\ 6 x^(6)+5x^(5)+2x^(4)-9x^(3)+7x^(2)-10x+2 - 6 x^(6) -2 x^(5) = 3x^(5)+2x^(4)-9x^(3)+7x^(2)-10x+2\\`

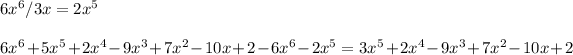
We repeat previous steps until we run out of numbers:

`3x^(5)/3x=x^(4) \\ \\ 3x^(5)+2x^(4)-9x^(3)+7x^(2)-10x+2-3x^(5)-x^(4)= \\ \\ x^(4)-9x^(3)+7x^(2)-10x+2 \\ \\ \\ x^(4)/3x= (1)/(3) x^(3) \\ \\ x^(4)-9x^(3)+7x^(2)-10x+2-x^(4)- (1)/(3) x^(3)= \\ \\ - (28)/(3) x^(3)+7x^(2)-10x+2 \\ \\ \\ - (28)/(3) x^(3)/3x= - (28)/(9) x^(2) \\ \\ - (28)/(3) x^(3)+7x^(2)-10x+2+ (28)/(3) x^(3)+ (28)/(9) x^(2) = \\ \\ (91)/(9) x^(2)-10x+2`

`(91)/(9) x^(2)/3x=(91)/(27) x \\ \\ (91)/(9) x^(2)-10x+2-(91)/(9) x^(2)-(91)/(27) x= \\ \\ -(361)/(27) x+2 \\ \\ \\ -(361)/(27) x/3x=-(361)/(81) \\ \\ -(361)/(27) x+2+(361)/(27)x+(361)/(27)= \\ \\ (415)/(27)`

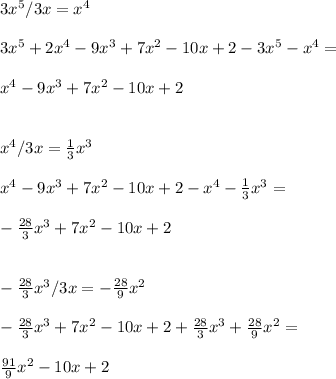
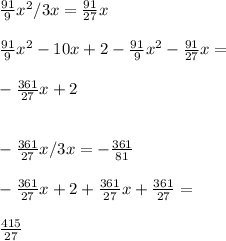
We are left with a number that has no x inside. This is remainder.
The final solution is sum of all these solutions and remainder:

`(2 x^(5)+x^(4)+(1)/(3) x^(3) - (28)/(9) x^(2) +(91)/(27) x)+(-(361)/(81) )`