Question

A manager receives 10 applications for a specific position. she wants to narrow it down to 3. in how many ways can she rank 3 applications?

Answer 1

To determine the number of ways a manager can rank 3 applications from a total of 10, one must calculate the permutations of 3 from 10, which is 10 factorial divided by (10-3) factorial. The result is 720 ways to rank the applications.

Step-by-step explanation:

The question is asking in how many different ways a manager can rank 3 applications from a total of 10 applications. This is a problem of permutations where order matters because ranking the applications means that the first place is different from second place, and so on.

To calculate this, we need to find the number of permutations of 3 applications out of 10, which is represented by the formula:

`Permutations = P(n, k) = \((n!)/((n-k)!)\)`

We have n = 10 applications, and we want to select k = 3 of them. Thus:

`P(10, 3) = \((10!)/((10-3)!) = (10!)/(7!) = 10 * 9 * 8 = 720`

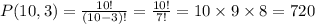
Therefore, there are 720 ways the manager can rank the 3 applications from the 10 applications received.

Answer 2

Experience. Background. Good work history.