Answer:
the area of a sector to the nearest hundredths is, 105.84 cm^2
Explanation:
Area of a sector(A) is given by:
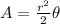 .....[1]
.....[1]
where,
r is the radius and
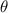 is the angle in radian.
is the angle in radian.
As per the statement:
a central angle of 3π/5 radians and a diameter of 21.2 cm
⇒
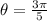
We know that:
Diameter(d) = 2(radius(r))
⇒
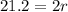
⇒
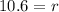
or
r = 10.6 cm
Substitute these in [1] we have;
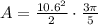
use 3.14 for π
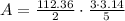
⇒
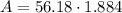
Simplify:
⇒
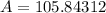 square cm
square cm
therefore, the area of a sector to the nearest hundredths is, 105.84 cm^2