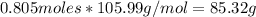Question

What mass of sodium carbonate would be required to remove essentially all of the calcium ion from 750 l of solution containing 43 mg ca2+ per liter?

Answer 1

Mass of Na2CO3 = 85.3 g

Step-by-step explanation:

Volume of solution, V = 750 L

Mass of Ca2+/L = 43 mg

Mass of Ca2+ = 40.08 g

Mass of Na2CO3 = 105.99 g/mol

The net ionic equation between Ca2+ and CO3^2- is:

`Ca^(2+) + CO3^(2-)  ------ CaCO_(3)`

Based on the stoichiometry:

1 mole of Ca2+ ions combines with 1 mole of CO₃²⁻ ions

Step 1: Calculate moles of Ca2+ in 750 L solution

Mass of Ca2+ in 750 L =
`(0.043 g * 750 L)/(1 L) = 32.25 g`

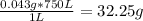
Moles of Ca2+ =
`(32.25 g)/(40.08 g/mol) =0.805 moles`

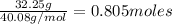
Step 2: Calculate the mass of Na2CO3 required

Moles of Ca2+ = Moles of Co3^2- = 0.805 moles

Mass of Na2CO3 =
`0.805 moles * 105.99 g/mol = 85.32 g`

Answer 2

Ca²⁺ reacts with CO₃²⁻ and forms CaCO₃. The reaction is
CO₃²⁻(aq) + Ca²⁺(aq) → CaCO₃(s)

First, let's find out the moles of Ca²⁺ in 750 L.
1 L has 43 mg of Ca²⁺
Hence, mass of Ca²⁺ in 750 L = 43 mg/L x 750 L
= 32250 mg = 32.25 g
Molar mass of Ca²⁺ = 40.078 g/mol
Hence, moles of Ca²⁺ in 750 L = mass / molar mass
= 32.25 g / 40.078 g/mol
= 0.8047 mol

The stoichiometric ratio between Ca²⁺ and CO₃²⁻ is 1 :1
Hence, moles of CO₃²⁻ = moles of Ca²⁺
= 0.8047 mol

CO₃²⁻ ions from dissociation of Na₂CO₃. The dissociation of Na₂CO₃ in water is
Na₂CO₃(s) → 2Na⁺(aq) + CO₃²⁻(aq)

The stoichiometric ratio between Na₂CO₃(s) and CO₃²⁻(aq) is 1 : 1
Hence, moles of Na₂CO₃(s) = moles of CO₃²⁻(aq)
= 0.8047 mol

Molar mass of Na₂CO₃ = 105.9888 g/mol
Hence, mass of Na₂CO₃ = moles x molar mass
= 0.8047 mol x 105.9888 g/mol
= 85.29 g

Hence, mass of Na₂CO₃ needed to react with Ca²⁺ is 85.29 g.