Answer:
The correct statements that is used to show that circle m is similar to circle n is:
- circle n is a dilation of circle m with a scale factor of 5.
- circle n is a translation of circle m, 1 unit right.
Explanation:
We know that two circles are said to be similar if by using some translation and some dilation it could be mapped to the other.
Circle m is given as:
circle m: center (−1, 10) and radius 3
That means the equation of circle m is:
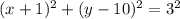
Circle n is given as:
circle n: center (0, 10) and radius 15
That means that the equation of circle n is:
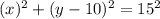
1)
circle n is a dilation of circle m with a scale factor of 5.
This option is correct.
Since, the radius of circle n is 5 times the radius of circle m.
2)
circle m and circle n are congruent.
This option is incorrect.
Since, the radius of both the circles are unequal and hence they can't be congruent.
3)
circle n is a translation of circle m, 1 unit right.
This option is correct.
Since, the center of circle m is: (-1,10)
and center of circle n is: (0,10)
That means m is to be shifted one unit to the right.
4)
circle m is a dilation of circle n with a scale factor of 12.
This option is incorrect.
Since circle m is a circle with smaller radius hence it can't be a dilation of circle n with scale factor greater than one.