5) So for parallelogram ABCD, ∠B ≅ ∠D, and ∠A ≅ ∠C. Further, ∠B and ∠A are supplementary (i.e., their sum is 180°), and ∠D and ∠C are also supplementary.
So, we have that m∠B = m∠D. Therefore,
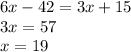
Now, let's substitute for x back into the expression for either ∠B or ∠D to find it's angle measure.
m∠B =
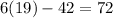
Now, remember that ∠B or ∠D are supplements of ∠A.
So, m∠B + m∠A = 180°.
That means m∠A = 180° – 72° = 108°.
That seems reasonable, because A appears to be an obtuse angle.