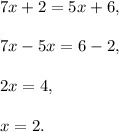Question

Use the drop-down menus to complete each equation so the statement about its solution is true

numbers in the drop box range from 0-9

Answer 1

No Solutions

5−4+7x+1= 7x + 5

One Solution

5−4+7x+1= 6x + 2

Infinitely Many Solutions

5−4+7x+1= 7x +2

Explanation:

Answer 2

1.
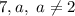`7, a,\ a\\eq 2` (for example, 7, 1);

2.
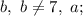`b,\ b\\eq 7,\ a;` (for example, 5, 6);

3.
`7,\ 2.`

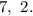
Explanation:

Simplify the given left side of each equation:

`5-4+7x+1=7x+(5-4+1)=7x+2.`

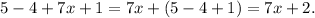
The equation

• has no solution if it is impossible for the equation to be true no matter what value we assign to the variable x;
• has infinitely many solutions if any value for the variable x would make the equation true;
• has exactly one solution.

No solutions: The right side of the equation should be of the form
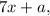`7x+a,` where
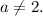`a\\eq 2.` For example,
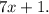`7x+1.` In this case, the equation will take look

`7x+2=7x+1,\\ \\ 2=1.`

This statement cannot be correct for any value of the variable x, so the equation has no solutions.

Infinitely many solutions: The right side should be exactly the same as the left side:

`7x+2=7x+2,\\ \\0=0.`

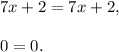
This statement is correct for all values of the variable x, so the equation has infinitely many solutions.

One solution: The right side of the equation should be of the form
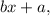`bx+a,` where
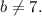`b\\eq 7.` For example,
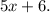`5x+6.` In this case,

`7x+2=5x+6,\\ \\7x-5x=6-2,\\ \\2x=4,\\ \\x=2.`