Question

Math teacher doesn't explain this very well, please help solve.

Answer 1

a) Since we know they have equal perimeters, we can set them equal to each other. First, let's recap the perimeters of squares and triangles (s = side):

`image`

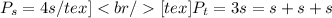
Now, we can set up our equation:

`4(x-3) = 8 + x + x`

`4x-12 = 8+2x`

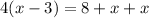
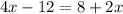
We can solve for x:

`2x-12=8`

`2x = 20`

`x = (20)/(2) = 10`

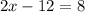
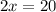
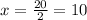
So, x = 10.

b) We known the perimeter formulas and we have what x is. So, let's just plug and chug.
Square:

`4(x-3) = 4(10-3) = 40-12 = 28`
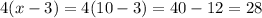
So, the perimeter of the square is 28 units².
Since their perimeters are equal the perimeter of the triangle is also 28 units²