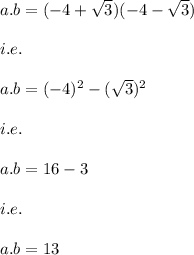Question

Let x = a and x = b be distinct solutions to the equation shown below. What is the exact value of a ⋅ b?

2(x + 4)^2 = 6

Answer 1

The exact value of a ⋅ b is:

13

Explanation:

The equation in terms of the variable x is given by:

`2(x+4)^2=6`

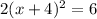
On diving both side of the equation by 2 we get:

`(x+4)^2=3`

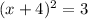
Also,

`(x+4)=\pm √(3)`

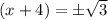
( Since, on taking square root on both the sides of the equation)

Hence, we get:

`x=-4\pm √(3)`

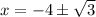
i.e.

`x=-4+√(3)`

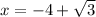
and

`x=-4-√(3)`

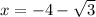
i.e.

`a=-4+√(3)\ and\ b=-4-√(3)`

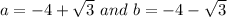
Hence,

`a.b=(-4+√(3))(-4-√(3))\\\\i.e.\\\\a.b=(-4)^2-(√(3))^2\\\\i.e.\\\\a.b=16-3\\\\i.e.\\\\a.b=13`

Answer 2

We have the following expression:
2 (x + 4) ^ 2 = 6
Let's clear the value of x:
x + 4 = +/- root (6/2)
x + 4 = +/- root (3)
x = +/- root (3) - 4
The solutions are:
a = root (3) - 4
b = -raiz (3) - 4
Multiplying both solutions we have:
a.b = (root (3) - 4) * (- root (3) - 4)
a.b = -9 -4raiz (3) + 4raiz (3) + 16
a.b = -9 + 16
a.b = 7
Answer:
the exact value of a ⋅ b is 7