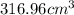Question

When the volume of a gas is changed from 524 cm^3 to ____ cm^3, the temperature will change from 491 K to 297 K .

Answer 1

V1/T1=V2/T2
524 cm^3/491 K =V2/297K

V2=(524 cm^3*297K)/491 K= 317K

Answer 2

Answer : The final volume of a gas is,
`316.96cm^3`

Explanation :

According to the Charles's law, the volume of a gas is directly proportional to the temperature of the gas at constant pressure and the number of moles of gas.

`V\propto T`

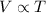
or,

`(V_1)/(V_2)=(T_1)/(T_2)`

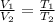
where,

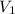`V_1` = initial volume of gas =
`524cm^3`

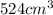
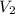`V_2` = final volume of gas = ?

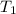`T_1` = initial temperature of gas = 491 K

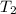`T_2` = final temperature of gas = 297 K

Now put all the given values in the above formula, we get the final volume of a gas.

`(524cm^3)/(V_2)=(491K)/(297K)`

`V_2=316.96cm^3`

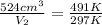
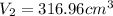
Therefore, the final volume of a gas is,
`316.96cm^3`