Question

Given quadrilateral RSTU, determine if each pair of sides (if any) are parallel and which are perpendicular for the coordinates of the vertices.

R(-l, -5), S(8, 2), T(5, 5), U(-4, -2)

the options are
a) parallel
b) perpendicular
c) none

Answer 1

We would need to figure out the gradient of each "pair", as provided in the image.

The equation of the gradient is found by,

m =
`( y_(2 ) - y_(1 ) )/( x_(2 ) - x_(1 ) )`

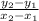
Parallel lines mean they have the same gradient
Perpendicular lines will follow the formula
`m_(1 ) * m_(2 ) = -1`
"None" will apply to those that do not follow either.

Now we calculate the gradient of the pairs given to us by substituting the x and y values.

RS =
`(2-5)/(8-(-1) )`
=
`-(1)/(3)`

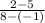
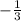
TU =
`(-2 - 5)/(-4 -5)`
=
`(7)/(9)`

Therefore, the "pair" RS and TU will be NONE.

ST =
`(5 - 2)/(5-8)`
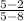
= -1

RU =
`(-2 -5)/(-4 -(-1) )`
=
`(7)/(3)`

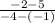
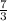
Therefore, the "pair" ST and RU is also NONE.

Hope this helped! Feel free to ask me if there's any part of the working you don't understand :)

Answer 2

RS -- a) is parallel to -- TU (by same slope = 7/9)
ST -- a) is parallel to -- RU (by same slope = -1)

Therefore it is a parallelogram, not a rectangle, because there are two sets of parallel lines, but each.set is not perpendicular to the other set. 7/9 is not the negative reciprocal of -1. It would have needed to.be 7/9 and -9/7, or -1 and +1.