Question

A toy rocket launched straight up from the ground with an initial velocity of 80 ft/s returns to the ground after 5 s. The height of the rocket t seconds after launch is modeled by the function f(t)=−16t^2+80t . What is the maximum height of the rocket, in feet? Enter your answer in the box.

Answer 1

Answer: it is 100 feet

Answer 2

The height of the rocket is modeled by the function:


`f(t)=-16 t^(2)+80t`

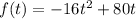
If we observe this equation, we see that the function is quadratic. The shape of the quadratic function is parabolic and the maximum or minimum value of a parabola always lies at its vertex. In the given function, since the co-efficient of leading term (t²) is negative, so this parabola will have a maximum value at its vertex.

The vertex of parabola is given by:


`( (-b)/(2a), f( (-b)/(2a)))`

b is the coefficient of t term. So b = 80
a is the coefficient of squared term. So a= - 16

So,


`(-b)/(2a)= (-80)/(2(-16))= (5)/(2)=2.5`

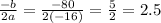
This means at 2.5 sec the height of rocket will be maximum. The maximum height will be:


`f(2.5)=-16 (2.5)^(2)+80(2.5)=100`

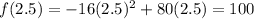Therefore, the maximum height of the rocket will be 100 feet.