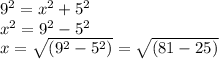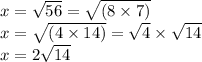the equation used to find the missing lengths:
9 = __SR (5^2 + x^2)__
As long as it is a right triangle, this is called the Pythagorean Theorem
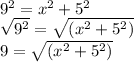
** FYI- if you wanted to SOLVE FOR THE MISSING SIDE X, then just switch around the original equation solving in terms of x: