Question

What is the coefficient of the x^5y^5-term in the binomial expansion of (2x -3y)10?

Answer 1

a answer is (2x−5y) and do the math 32x5−400x4y+2000x3y2−5000x2y3+6250xy4−3125y5

Answer 2

The coefficient of
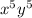`x^5y^5` is (-1959552).

Explanation:

Given : Expression
`(2x-3y)^(10)`

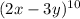
To find : What is the coefficient of the term
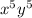`x^5y^5` in the binomial expansion of expression ?

Solution :

The binomial expansion is
`(x+y)^n=\sum ^nC_k x^(n-k) y^k`

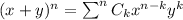
Where,
`^nC_k=(n!)/((n-k)!k!)`

On comparison with given expression
`(2x-3y)^(10)`

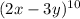
x=2x , y=-3y and n=10, k=0,1,.....,10.

Substituting in the formula and expand,

`(2x-3y)^(10)=\sum ^(10)C_k (2x)^(10-k) (-3y)^k`

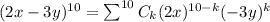
`(2x-3y)^(10)=^(10)C_0(2x)^(10-0) (-3y)^0+^(10)C_1(2x)^(10-1) (-3y)^1+^(10)C_2(2x)^(10-2) (-3y)^2+^(10)C_3(2x)^(10-3) (-3y)^3+^(10)C_4(2x)^(10-4) (-3y)^4+^(10)C_5(2x)^(10-5) (-3y)^5+^(10)C_6(2x)^(10-6) (-3y)^6+^(10)C_7(2x)^(10-7) (-3y)^7+^(10)C_8(2x)^(10-8) (-3y)^8+^(10)C_9(2x)^(10-9) (-3y)^9+^(10)C_(10)(2x)^(10-10) (-3y)^{10]`

`(2x-3y)^(10)=1024x^(10)-15360x^9y+103680x^8y^2-414720x^7y^3+1088640x^6y^4-1959552x^5y^5+2449440x^4y^6-2099520x^3y^7+1180980x^2y^8-393660xy^9+59049y^(10)`

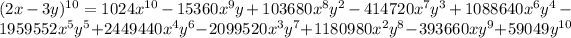
So, The coefficient of
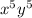`x^5y^5` is (-1959552).