Question

You have 1500 and want to invest it for the future. Bank of westminster has a saving account with an interest rate of 3% compounded yearly, but a local credit union is offering 2% compounded continuously. Which account would give you more money if you leave the money in the account for 10 years? How much more? Show all calculation and label everything

Answer 1

Principal amount = P = $1500
Time in years = t =10
For annual compounding, interest rate = r = 3% = 0.03
Amount accumulated = A

Formula for Annual(Yearly) compounding is: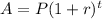


`A=P (1+r)^(t)`

Using the values, we get:


`A=1500(1+0.03)^(10)=2015.87`

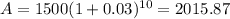
Interest rate for continuous compounding = r = 2% = 0.02

Formula for continuous compounding is: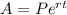


`A=P e^(rt)`

Using the values, we get:


`A=1500 e^(0.02*10)=1832.10`

This means amount accumulated by yearly compounding after 10 years will be $ 2015.87 and amount accumulated by continuous compounding will be $ 1832.40. Therefore the amount with yearly compounding will have more amount by the end of 10th year. The difference in the two amounts will be $183.47. So the yearly compounding will have saved $183.47 more than continuous compounding.