9514 1404 393
Answer:
y^6
Explanation:
It can help to remember that an exponent is simply an indicator of repeated multiplication. Common factors cancel from numerator and denominator.
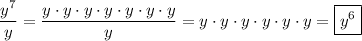
_____
Written as a rule of exponents, this is ...
(a^b)/(a^c) = a^(b-c)
Of course, a = a^1.