Question

What is the length of AC?

Answer 1

7/x = 84 / (156 -x)
84x = 7(156 -x)
84x = 1092 - 7x
91x = 1092
x = 12

AC = 156 - 12 = 144

answer
D. 144

Answer 2

In the given diagram, We are given two right triangles BAC and DEC.

Triangle BAC has right angle at A and triangle DEC has right angle at E.

Also we are given <BCA ≅<DCA.

Therefore,

Triangle BAC is similar to triangle DEC by Angle Angle similarity theorem.

Note: The sides of similar triangles are in proportion.

Therefore,

`(AB)/(ED) = (AC)/(EC)`

`(84)/(7)=(156-x)/(x)`

`\mathrm{Apply\:fraction\:cross\:multiply:\:if\:}(a)/(b)=(c)/(d)\mathrm{\:then\:}a\cdot \:d=b\cdot \:c`

`84x=7\left(156-x\right)`

`84x=1092-7x`

`\mathrm{Add\:}7x\mathrm{\:to\:both\:sides}`

`84x+7x=1092-7x+7x`

`91x=1092`

`\mathrm{Divide\:both\:sides\:by\:}91`

`(91x)/(91)=(1092)/(91)`

`x=12`

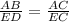
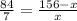
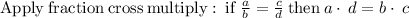
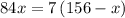
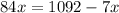
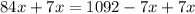
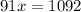
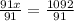
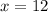
AC = 156 -x.

Plugging value of x in 156-x, we get

156-12 = 144.

Therefore, AC = 144 units.

Correct option is D. 144.