So, we are going to use the compound interest formula:
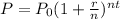
where

is the final amount
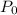
is the initial amount

is the interest rate in decimal form

is the number of times the interest is compounded per year

is the time in years
Since in all the cases
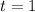
, we can omit

.
1. Once per year. In this case:

,
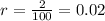
, and
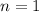
. Lets replace those values in our formula:
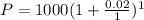
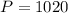 2. Every three months.
2. Every three months. In this case:
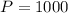
,
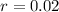
, and
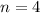
. Lets replace those values in our formula:

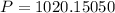 3. Every month.
3. Every month. In this case:
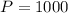
,
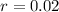
, and

. Lets replace those values in our formula:
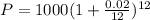
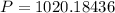 4. Every week.
4. Every week. In this case:
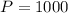
,
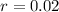
, and

. Lets replace those values in our formula:
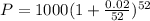
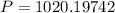 5. Every day.
5. Every day. In this case:
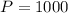
,
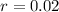
, and
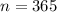
. Lets replace those values in our formula:
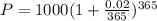

We can conclude that

increases as

increases.