Question

Use the numbers from the original example: $1,000 invested at a 2% interest rate compounded n times per year. Compare the change in P as n increases. Fill in the table. Use a calculator and write the values to 5 decimal places. Use commas in your answer when necessary.

n
P=P0(1+r/n)^n
1 (once per year)
a0
4 (every 3 months)
a1
12 (every month)
a2
52 (every week)
a3
365 (every day)
a4

Answer 1

So, we are going to use the compound interest formula:
`P=P_(0)(1+ (r)/(n) )^(nt)`
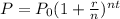
where

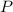
`P` is the final amount

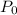
`P_(0)` is the initial amount

`r` is the interest rate in decimal form

`n` is the number of times the interest is compounded per year

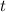
`t` is the time in years
Since in all the cases
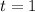
`t=1`, we can omit
`t`.

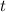
1. Once per year. In this case:
`P_(0)=1000`,
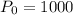
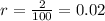
`r= (2)/(100) =0.02`, and
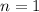
`n=1`. Lets replace those values in our formula:

`P=1000(1+ (0.02)/(1) )^(1)`

`P=1020`

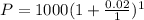
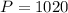2. Every three months. In this case:
`P=1000`,
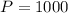
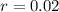
`r=0.02`, and
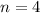
`n=4`. Lets replace those values in our formula:

`P=1000(1+ (0.02)/(4) )^(4)`

`P=1020.15050`

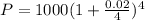
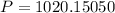3. Every month. In this case:
`P=1000`,
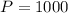
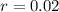
`r=0.02`, and
`n=12`. Lets replace those values in our formula:

`P=1000(1+ (0.02)/(12) )^(12)`

`P=1020.18436`

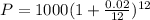
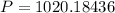4. Every week. In this case:
`P=1000`,
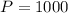
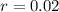
`r=0.02`, and
`n=52`. Lets replace those values in our formula:

`P=1000(1+ (0.02)/(52) )^(52)`

`P=1020.19742`

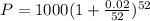
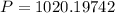5. Every day. In this case:
`P=1000`,
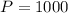
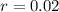
`r=0.02`, and
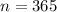
`n=365`. Lets replace those values in our formula:

`P=1000(1+ (0.02)/(365) )^(365)`

`P=1020.20078`

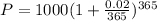
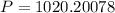
We can conclude that
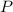
`P` increases as
`n` increases.